CASTEP calculations using Materials Studio
This protocol was influenced by separate, independently prepared, guides written by Sten Nilsson Lill (AstraZeneca, Sweden) and Albert Bartók-Pártay (Science and Technology Facilities Council, UK), in addition to stress-testing of parameters using a starting input of the crystal structure of β-piroxicam (CSD refcode: BIYSEH03)1. The settings suggested herein are applicable to 1H, 13C, 15/14N and 17O. If the calculation does not run using the parameters specified within the main body of the text, troubleshooting guidance can be found in A8.
Materials Studio, version 17.1.0.48 is used throughout this guide. Minor differences in other versions of the software are possible.
- Create a New Project in Materials Studio
- Select .cif file for input:
- Cambridge Crystallographic Data Centre website
- ConQuest Search (see Fig. 1)
- existing .cif file from personal folder
- Import .cif file and verify that structure is as expected.
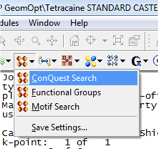
In some cases the structure solution does not add hydrogen atoms to the structure. These can be added to the structure by Build > Crystals > Unbuild Crystal, followed by Build > Crystals > Rebuild Crystals. Furthermore, ensure that the bonding configuration is as expected. To change the visualization of bonding go to Build > Bonds, and choose Kekule or Resonant, although this is for visualization purposes only and will not alter the calculated result.
This step is considered necessary before any NMR calculation. All atoms are typically allowed to relax during the geometry optimization step. Details on how to perform a relaxation of selected atoms only can be found in the Appendix. With the structure required to be optimized open, navigate to the CASTEP module as indicated in Fig. 2.
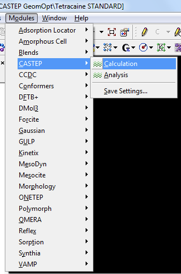
A window with four tabs is loaded. A brief explanation, and suggested input values, for selected fields are given below:
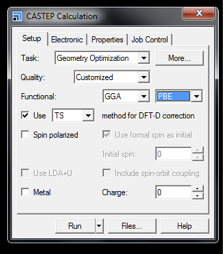
- Task is Geometry Optimization
- Quality: Customised – as we will see later this drop-down will automatically change to this value as we modify further input parameters
- Functional: Use GGA and PBE
- Method for DFT-D correction: TS. TS has been found to give greater precision in cell parameters.2 Inclusion of a DFT-D correction term is crucial if unit cell parameters are allowed to relax. Inclusion of a DFT-D correction is not considered critical for accurate calculated NMR parameters if unit cell parameters are fixed, however the inclusion of a correction with fixed unit cell parameters will not have any adverse effects on the outputted NMR values or computational time and is therefore recommended.
- Ensure that the Spin polarized and Metal box are unticked. By default, Metal box will be ticked when the CASTEP module is first opened.
Clicking More... loads additional options.

- Quality specifies the tolerances that the Geometry Optimization must satisfy to successfully complete. A value of Fine is typically sufficient (see the Appendix for piroxicam testing, Table A2). The numerical convergence tolerance values associated with each quality description within Materials Studio are specified in the Appendix.
- If performing a more demanding optimization (e.g., smaller tolerance values, varying of unit cell parameters, high number of atoms in unit cell) then a higher number of iterations may be need. Setting the number of iterations to 500 should be sufficient for any typical parameter set or input structure. Further troubleshooting guidance can be found in the Appendix, section A8.
- Inclusion of ‘Optimize cell’ is optional. If confident in the unit cell parameters then this box can be unticked. However, if you wish to optimize the cell then a dispersion correction, as discussed previously, must be included. The user should consider that optimizing the cell parameters increases the calculation time.
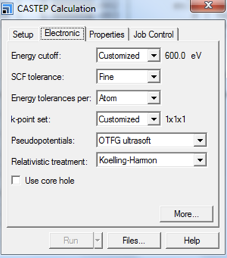
- Energy cutoff can be chosen as either an option from the drop-down menu, or specified by the user. A value of 600 eV (see A3 for further details), specified by the user in the More... button (see Fig. 6 for further instructions) is advised. Note, at the time of writing this applies when studying lighter nuclei, e.g., 1H, 13C, 14N, 15N.
- SCF tolerance should be set to Fine. Numerical values for each descriptive term for SCF tolerance can be found in A4.
- Energy Tolerances per: Atom.
- k-point set: Customized, the value will be set later using the More... button
- Pseudopotentials: OTFG ultrasoft (On the Fly Generated Pseudopotentials)
- Relativistic Treatment: Koelling-Harmon
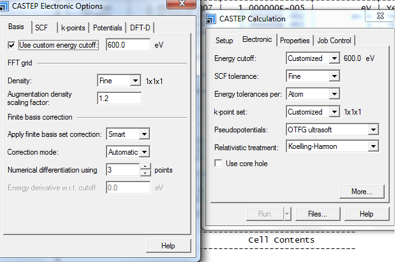
The More... button loads a pop-up with 5 tabs (Fig. 6 and Fig. 7).

- In the Basis tab the custom energy cutoff can be set. As discussed, 600 eV is advised. All other parameters in this tab can be left as default (see Fig. 6).
- In the k-points tab, Separation can be set to 0.05. See the A5 for further details. No further modifications are required in the remaining tab options.
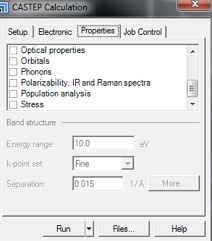
- Population analysis should be unticked (by default it may be ticked).
- For a geometry optimization no boxes should be ticked.
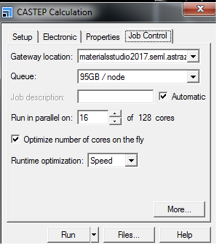
- Gateway location should be a suitable server to handle a job of this kind.
- By ticking Optimize number of cores on the fly this can be automatically adjusted for most efficient calculations.
- Runtime Optimization: options are Default, Speed and Memory. For most cases Speed is most suitable. For larger systems that have increased memory requirements the Memory option may be preferable.
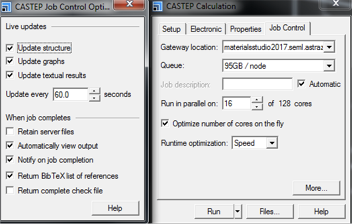
In the More... setting the options shown in Fig. 10 are available.
- Live updates boxes ticked provide useful visual insight into the progress of a calculation.
- Retain server files is not usually required.
- Return check file is not required.
- Return BibTex list of references provides references for any publication, so is not required for all runs, but it may be useful to have a copy of this file generated once for future use.
The remaining tick boxes are at the users discretion and do not alter the calculated result or computational requirements.
Click Run to begin the job. Note, do not change the name of job title folder during the calculation, as this will mean that the calculation will not know the location to download the files. Once the job has successfully completed numerous output files are available:

- (A) .param file. Contains information detailing the type of calculation performed and the parameters that were used during the calculation.
- (B) The .xsd structure is the updated structure after geometry optimization. From here, the user can launch the CASTEP GIPAW calculation. Furthermore, this file can be exported as a .cif file for comparison to other files (e.g., the original .cif file, geometry optimized structures generated using different input parameters) using suitable external software.3
- (C) .xst structure is the original input structure.
- (D) opens the CASTEP module window. This is for reference purposes only, changing any parameters here after the launch of the calculation will not alter the result. It is recommended that the values are not altered, and the values herein are therefore maintained as a useful reference to parameters used. However, definitive parameters used can be found in the .castep file (H).
- (E) The Status file. Details the progression of the calculation.
- (F) Graphical representation of the convergence of the energy with each geometry optimization step. The energies graph should not oscillate significantly and should converge after a suitable number of steps (the number of steps will depend on the input system and parameter set specified). If any minor oscillations are observed then the convergence should be the lowest point of the oscillation.
- (G) Graphical representation of the convergence of the geometry optimization tolerance values with each geometry optimization step. If the unit cell is fixed 3 convergence values are shown (Max Force, Max Displacement, Energy Change). If the unit cell is allowed to relax then a Max Stress parameter is also included.
- (H) The .castep file gives all information concerning the calculation. At the end of the document the calculation time and efficiency are given. These values will provide a useful reference for comparison to previous or upcoming geometry optimization calculations. Lines ending in
<-- SCFdescribe electronic structure convergence, and lines ending in<-- BFGSdescribe geometry optimization convergence. Furthermore, the final energy after convergence can be found towards the end of the .castep file. Any problems encountered during the calculation can also be identified within this file. Warning messages are explicitly stated within the .castep file.
Open the geometry optimized xsd file found within the Geometry Optimization subfolder (item (B) in Fig. 11). Click Modules > CASTEP > Calculation.
- Change Task to Energy
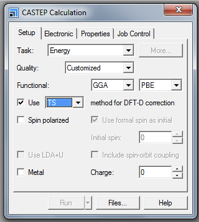
NOTE: as of Materials Studio version 17.1.0.48 it is also possible to run an NMR calculation by selecting Properties from the task dropdown menu, however this is not recommended as settings specified during the geometry optimization step will be used, regardless of what is stated in the calculation details and status file.
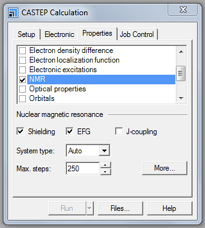
- ensure that NMR is ticked
- and the interactions required are ticked (usually a minimum of Shielding and EFG). J-coupling calculations are time consuming and therefore should only be included if required.
- The cutoff energy may be increased, a value of 700 eV should be sufficient for 1H, 13C, 14N, 15N. See A6.
- k-point spacings are usually kept to the same value as for the geometry optimization, Separation: 0.05. See A7.
- Runtime Optimization can be set to Speed for most cases.
Upon successful completion of the calculation, numerous output files are available within Materials Studio. Within the .castep file, the outputted NMR parameters are found towards the end of the document (file labelled (I) in Fig. 14). Alternatively, NMR parameters can be extracted from the .magres file.
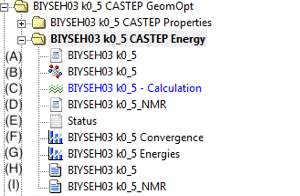
- (A) Energy .param file. Contains information detailing the type of calculation performed and the parameters that were used during the calculation.
- (B) The .xsd structure is the updated structure after geometry optimization.
- (C) opens the CASTEP module window. This is for reference purposes only, changing any parameters here after the launch of the calculation will not alter the result. It is recommended that the values are not altered, and the values herein are therefore maintained as a useful reference to parameters used. However, definitive parameters used can be found in the .castep file (H) and (I).
- (D) NMR .param file. Contains information detailing the type of calculation performed and the parameters that were used during the calculation.
- (E) Status file. Details the progression of the calculation.
- (F) Graphical representation of the convergence of the Energy per Atom (eV/atom).
- (G) Graphical representation of the convergence of the Total Energy (eV).
- (H) The .castep file gives all information concerning the Energy calculation.
- (I) The .castep file gives all information concerning the NMR calculation. Shielding and EFG values can be found here.
The .magres file is not displayed within Materials Studio. It is found in the relevant explorer folder where Materials Studio jobs are specified within a full list of generated files. The .magres file is useful for visualisation and analysis of the NMR calculated output using MagresView and MagResPython.4 Furthermore, full tensor values are included in the .magres file. The .magres file may be a hidden file, so it may be necessary to change the appropriate settings in Folder Options for access. The MagresView program can be downloaded to be used offline, or used within a browser. Software and user guides can be found on the CCP-NC website.
A CASTEP NMR calculation outputs the absolute chemical shielding. For comparison to experimental data this must be converted to a scale comparable to the experimental chemical shift (i.e., TMS = 0 ppm for 1H and 13C). To achieve this a reference value (σref) must be found. σref is calculated from the sum of the mean average of the experimental isotropic chemical shifts and the mean average of the calculated absolute shieldings. Typical values for different nuclei are as follows: 1H: 30 ppm, 13C: 170 ppm, 17O: 255 ppm, 15N: −160 ppm, and may be used in the absence of reliable experimental data. Any significant deviation away from these values indicates a possible problem with your calculation, and the input and output files should be carefully inspected for problems or inconsistencies. Isolated discrepancies between experiment and calculation are often related to local dynamics or temperature effects not included in the calculation.
A limiting factor is that high ppm regions in 13C spectrum (e.g., carboxyl groups) and lower ppm regions (e.g., methyl groups) may produce different values of σref. One approach is to calculate separate σref values for resonances above and below 100 ppm. If a single value is applied this may explain discrepancy between experiment and calculated chemical shift values in different spectral regions. Alternative methods for converting from the absolute chemical shielding scale are possible, and are discussed elsewhere.56
Below, the setup steps prior to launching the Modules > CASTEP > Calculation step are shown. In order to optimize only the hydrogen atoms the heavier atoms need to be selected and their positions fixed. This is achieved as follows: Open Edit > Atom Selection. Atoms that are not to be optimized are selected. Criteria for property and specifications are given in the top dropdown menus. In Fig. A1, only H atoms are to be optimized, therefore atoms are selected by property, and all atoms that are not H are selected.
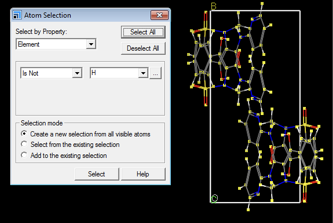
Afterwards, open Modify > Constraints and ensure that Fix Cartesian position and Fix fractional position are ticked. This fixes the position of all non-hydrogen atoms selected.
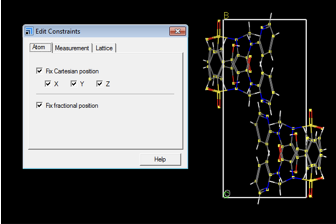
Perform the CASTEP Geometry Optimization and CASTEP NMR calculation as described in the main body of the text.
Piroxicam (BIYSEH03)
Table A1: Numerical values associated with each geometry optimization tolerance value.
a The energy referred to herein is the convergence energy threshold permitted between each geometry optimization step, and should not be confused with the SCF tolerance energy, which is described in Table A4.
| Quality | Forces / eV Å-1 | Stresses / GPa | Energies / eV a | Displacements / Å |
|---|---|---|---|---|
| Coarse | 0.1 | 0.2 | 5 \(\cdot\) 10-5 | 5 \(\cdot\) 10-3 |
| Medium | 0.05 | 0.1 | 2 \(\cdot\) 10-5 | 2 \(\cdot\) 10-3 |
| Fine | 0.03 | 0.05 | 1 \(\cdot\) 10-5 | 1 \(\cdot\) 10-3 |
| Ultra-fine | 0.01 | 0.02 | 1 \(\cdot\) 10-6 | 5 \(\cdot\) 10-4 |
Table A2: σref values and average difference between experimental and calculated shifts obtained for 1H and 13C for different quality values for the geometry optimization tolerance.
a Geometry optimization was performed using a plane wave basis cut off energy of 600 eV and a k-point spacing of 0.05 Å-1. NMR calculations were performed using a PBE functional with plane wave basis cutoff energy of 700 eV and k-point spacing of 0.05 Å-1.
b RMSD is relative to non-optimized structure (BIYSEH03 .cif file extracted from CSD).
| Quality | σref(1H) / ppm a | \(\delta\)exp-\(\delta\)calc (1H) / ppm a | σref(13C) / ppm a | \(\delta\)exp-\(\delta\)calc (13C) / ppm a | RMSD / Å b | Final Energy / eV |
|---|---|---|---|---|---|---|
| Coarse | 30.7 | 0.6 | 170.3 | 1.9 | 0.075 | -21854.48 |
| Medium | 30.7 | 0.6 | 170.3 | 1.7 | 0.111 | −21854.64 |
| Fine | 30.6 | 0.6 | 170.4 | 1.7 | 0.148 | −21854.71 |
| Ultra-fine | 30.7 | 0.6 | 170.2 | 1.7 | 0.152 | −21854.72 |
Root Mean Square Displacement (RMSD) values were calculated using Mercury, and correspond to the root mean square difference in position between the non-optimized structure and the geometry-optimized structure using the parameter set specified in the table. A convergence of this value with respect to the parameter selected to be varied indicates that the configuration of the atoms does not significantly change as the selected parameter is changed.
Piroxicam (BIYSEH03)
Table A3: σref values and average difference between experimental and calculated shifts obtained for 1H and 13C for different plane wave basis cutoff energy values during geometry optimization.
a Geometry optimization was performed using a k-point spacing of 0.05 Å-1 and geometry optimization tolerance levels set to fine. NMR calculations were performed using a PBE functional with plane wave basis cutoff energy of 700 eV and k-point spacing of 0.05 Å-1.
b RMSD is relative to non-optimized structure (BIYSEH03 .cif file extracted from CSD)
c Agreement is poor and meaningful overlay is not possible in Mercury.
| Plane-wave basis cutoff energy / eV | σref(1H) / ppm a | \(\delta\)exp-\(\delta\)calc (1H) / ppm a | σref(13C) / ppm a | \(\delta\)exp-\(\delta\)calc (13C) / ppm a | RMSD / Å b | Final Energy / eV |
|---|---|---|---|---|---|---|
| 300 | 29.8 | 1.8 | 193.1 | 3.2 | N/A c | −21685.59 |
| 400 | 30.6 | 0.6 | 177.1 | 1.5 | 0.137 | −21818.19 |
| 500 | 30.6 | 0.6 | 171.6 | 1.6 | 0.144 | −21848.84 |
| 600 | 30.7 | 0.6 | 170.4 | 1.7 | 0.148 | −21854.71 |
| 700 | 30.7 | 0.5 | 170.3 | 1.7 | 0.148 | −21855.54 |
| 800 | 30.7 | 0.5 | 170.3 | 1.7 | 0.147 | −21855.58 |
Table A4: Numerical values associated with each SCF tolerance description. The SCF tolerance value is the targeted maximum change in total energy between each iteration of the electronic self-consistent field minimisation, and must be achieved over 3 successive steps (default value is 3 steps) for convergence to be considered successful. The SCF tolerance value should always have a smaller threshold value than the geometry optimization energy threshold value.
| SCF tolerance description | SCF tolerance value / eV |
|---|---|
| Coarse | 1 \(\cdot\) 10-5 |
| Medium | 2 \(\cdot\) 10-6 |
| Fine | 1 \(\cdot\) 10-6 |
| Ultra-fine | 5 \(\cdot\) 10-7 |
Table A5: σref values and average difference between experimental and calculated shifts obtained for 1H and 13C for different k-point spacing during geometry optimization.
a Geometry optimization was performed using a plane wave basis cut-off energy of 600 eV and geometry optimization tolerance levels set to fine. NMR calculations were performed using a PBE functional with plane wave basis cutoff energy of 700 eV and k-point spacing of 0.05 Å-1.
b RMS is relative to non-optimized structure (BIYSEH03 .cif file extracted from CSD).
c These k-point spacing values (0.5 Å-1 , 0.2 Å-1 , 0.1 Å-1 ) for this molecule all produce the same k-point grid.
| k-point spacing / Å-1 | k-point grid | σref(1H) / ppm a | \(\delta\)exp-\(\delta\)calc (1H) / ppm a | σref(13C) / ppm a | \(\delta\)exp-\(\delta\)calc (13C) / ppm a | RMSD / Å b | Final Energy / eV |
|---|---|---|---|---|---|---|---|
| 0.5c | (111) | 30.6 | 0.6 | 169.8 | 3.0 | 0.149 | −21854.87 |
| 0.2c | (111) | 30.6 | 0.6 | 169.8 | 2.9 | 0.147 | −21854.87 |
| 0.1c | (111) | 30.7 | 0.6 | 169.8 | 2.9 | 0.148 | −21854.87 |
| 0.07 | (211) | 30.7 | 0.6 | 170.4 | 1.7 | 0.152 | −21854.72 |
| 0.05 | (311) | 30.7 | 0.6 | 170.4 | 1.7 | 0.148 | −21854.71 |
Piroxicam (BIYSEH03)
Table A6: σref values and average difference between experimental and calculated shifts obtained for 1H and 13C for different plane wave basis cutoff energy values during CASTEP NMR calculations.
a BIYSEH03 was geometry optimized prior to CASTEP NMR calculation using a PBE functional with plane wave basis cutoff energy of 600 eV and k-point spacing of 0.05 Å-1. NMR calculations were performed using a PBE functional and a k-point spacing of 0.05 Å-1 .
| Plane-wave basis cutoff energy / eV | σref(1H) / ppm a | \(\delta\)exp-\(\delta\)calc (1H) / ppm a | σref(13C) / ppm a | \(\delta\)exp-\(\delta\)calc (13C) / ppm a |
|---|---|---|---|---|
| 300 | 29.5 | 0.4 | 197.5 | 2.3 |
| 400 | 30.2 | 0.5 | 177.3 | 1.2 |
| 500 | 30.4 | 0.5 | 171.7 | 1.5 |
| 600 | 30.6 | 0.6 | 170.4 | 1.6 |
| 700 | 30.7 | 0.6 | 170.3 | 1.6 |
| 800 | 30.8 | 0.6 | 170.3 | 1.4 |
Piroxicam (BIYSEH03)
Table A7: σref values and average difference between experimental and calculated shifts obtained for 1H and 13C for different k-point spacing values during CASTEP NMR calculations.
a BIYSEH03 was geometry optimized prior to CASTEP NMR calculation using a PBE functional with plane wave basis cutoff energy of 600 eV and k-point spacing of 0.05 Å-1 . NMR calculations were performed using a PBE functional and a plane wave basis cutoff energy of 700 eV.
b These k-point spacing values (0.5 Å-1, 0.2 Å-1, 0.1 Å-1) for this molecule all produce the same k-point grid.
| k-point spacing / Å-1 | σref(1H) / ppm a | \(\delta\)exp-\(\delta\)calc (1H) / ppm a | σref(13C) / ppm a | \(\delta\)exp-\(\delta\)calc (13C) / ppm a |
|---|---|---|---|---|
| 0.5 | 30.7 | 0.7 | 169.7 | 3.3 |
| 0.2 | 30.6 | 0.7 | 169.7 | 3.3 |
| 0.1 | 30.7 | 0.7 | 169.7 | 3.3 |
| 0.07 | 30.7 | 0.6 | 170.3 | 1.7 |
| 0.05 | 30.7 | 0.6 | 170.3 | 1.6 |
If the calculation fails to complete the source of the failure can be found in the .castep file.
Ensure that the number of iterations is sufficient relative to the geometry optimization tolerance values, smaller tolerance values will require a higher number of iterations. The number of iterations is changed in the Setup tab followed by the More... button (see Fig. 4).
If performing a calculation for a model with a high number of atoms (>400), a Monkhorst-Pack grid with k-point spacing of 0.1 Å-1, which will usually result in a single k-point (this should be confirmed), will reduce the memory requirements of the calculation. A lower k-point spacing (<0.1 Å-1) may be too demanding from a memory requirement point of view. Runtime Optimization in the Job Control tab can be changed to Default or Memory.
The protocol described here is a product of a collaborative effort of the following:
- Andrew S. Tatton and Jonathan R. Yates, Department of Materials, Oxford University, Oxford, UK
- Les Hughes and Helen Blade, Pharmaceutical Development, AstraZeneca, Macclesfield, UK
- Sten Nilsson Lill, Early Product Development, AstraZeneca, Mölndal, Sweden
- Albert Bartók-Pártay, STFC Scientific Computing Department, Rutherford Laboratory, Didcot, UK
- Steven P. Brown, Department of Physics, University of Warwick, Coventry, UK
- Paul Hodgkinson, Department of Chemistry, Durham University, Durham, UK
Andrew S. Tatton performed the calculations and prepared this document.
-
Agam R. Sheth, Simon Bates, Francis X. Muller and David J. W. Grant, Crystal Growth & Design 5, 571 (2005) ↩
-
Dmytro V. Dudenko, Jonathan R. Yates, Kenneth D. M. Harris and Steven P. Brown, CrystEngComm 15, 8797 (2013) ↩
-
I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Cryst. B58, 389 (2002) ↩
-
Simone Sturniolo, Timothy F.G. Green, Robert M. Hanson, Miri Zilka, Keith Refson, Paul Hodgkinson, Steven P. Brown, Jonathan R. Yates, Solid State Nucl. Magn. Reson. 78, 64, (2016) ↩
-
Robin K. Harris, Paul Hodgkinson, Chris J. Pickard, Jonathan R. Yates and Vadim Zorin, Magn. Reson. Chem. 45, S174 (2007) ↩
-
G.N. Manjunatha Reddy, Daniel S. Cook, Dinu Iuga, Richard I. Walton, Andrew Marsh, Steven P. Brown, Solid State Nucl. Magn. Reson. 65, 41 (2015) ↩